常用的机器人导航算法中求取最短路径的算法除了A算法以外,Dijstra(迪杰克斯拉)算法也是广泛使用的一种算法。通常来说,A搜索效率较高,而Dijstra的算法简单,较容易得出最小路径的长度。
算法推演
Dijstra算法主要用于求得一个点到其余各个点之间的最短路径。如图所示,应用场景可以如下,已知多个城镇之间的交通时间,求得源城镇A到目标城镇的最短时间。设定中路径可以为单程,各箭头数字表示1点到达2点的时间耗费。计算从A到G的最短耗费。
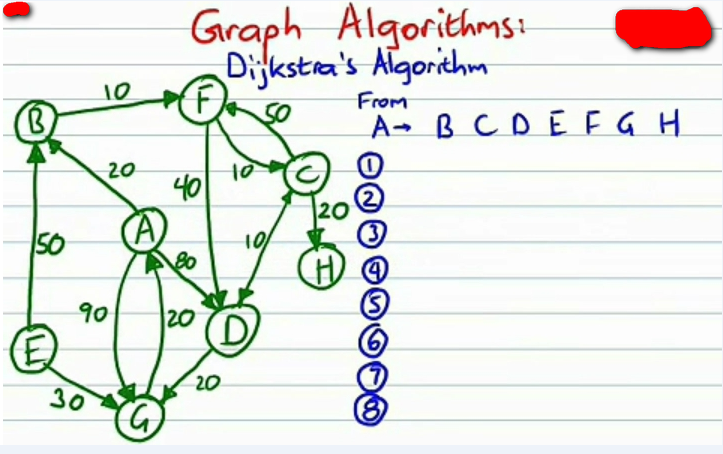
0
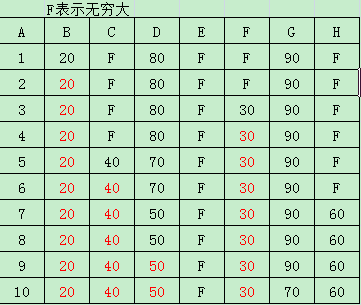
首先:先计算从A到其他各点的耗费值dis(a,x),无法直连的设为无穷大,用F表示。

1
第二:选择各点距离中最小值,并将最小值加入已阅列表。如图中B点。
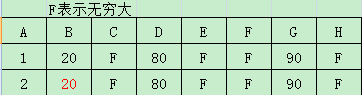
2
第三:计算上次选择的最小值B点到其他点的耗费dis(b,x),比较原来A点到其他各点耗费dis(a,x)与dis(a,b)+dis(b,x),当dis(a,x)>dis(a,b)+dis(b,x)时,可以认为通过B点中转的路径优与直行路径,从而设定dis(a,x)=dis(a,b)+dis(b,x)。此过程也称之为松弛。
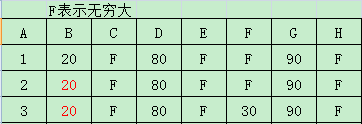
3
第四,同样的选择除已阅列表以外的所有值中最小的值F,并将F加入已阅列表,对再F进行松弛
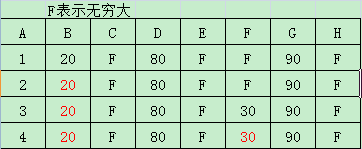
4
第五,重复进行选择最小值,松弛的工作,直到所有点松弛完毕。
5
算法实现步骤
由上述推演可知,实现Dijstra算法的主要步骤如下:
1 选择起点start与终点goal
2 所有点除起点外加入开启列表,并将起点加入关闭列表
3 初始化计算,更新起点与其他各点的耗费dis(start,n)
- 开启列表中,选择dis(start,n)中值最小的点x
- 将x加入关闭列表
- 对于剩余列表中,计算dis(start,n)>dis(start,x)+dis(x,n)
若真则dis(start,n)=dis(start,x)+dis(x,n),此时start与n点路径经过x点。 - 循环直至goal点加入开启列表,取得dis(start,goal)即为最短距离
Dijstra算法编程实现
#!/usr/bin/env python
#coding:utf-8
def dij(G,start,end):
dis={}
visited={}
father={}
Path = []
for x in G:
dis[x]=G[start][x]
visited[x]=0
if dis[x]<F:
father[x]=start
visited[start]=True
for y in G:
min=F
for z in G[y]:
if not visited[z] and dis[z]<min:
min=dis[z]
min_i=z
visited[min_i]=True
for w in G:
if not visited[w] and (dis[w]>dis[min_i]+G[min_i][w]):
dis[w]=dis[min_i]+G[min_i][w]
father[w]= min_i
cost=dis[end]
while 1:
Path.append(end)
if end == start: break
end = father[end]
Path.reverse()
return (Path,cost)
F=9999
G={ 'a':{'a':0,'b':20,'c':F,'d':80,'e':F,'f':F,'g':90,'h':F},
'b':{'a':F,'b':0,'c':F,'d':F,'e':F,'f':10,'g':F,'h':F},
'c':{'a':F,'b':F,'c':0,'d':10,'e':F,'f':50,'g':F,'h':20},
'd':{'a':F,'b':F,'c':F,'d':0,'e':F,'f':F,'g':20,'h':F},
'e':{'a':F,'b':50,'c':F,'d':F,'e':0,'f':F,'g':30,'h':F},
'f':{'a':F,'b':F,'c':10,'d':40,'e':F,'f':0,'g':F,'h':F},
'g':{'a':20,'b':F,'c':F,'d':F,'e':F,'f':F,'g':0,'h':F},
'h':{'a':F,'b':F,'c':F,'d':F,'e':F,'f':F,'g':F,'h':0}
}
print dij(G,'a','g')