@[TOC](2.25机器学习数学基础笔记之二)
1. 凸函数的判定(开口往上凸函数 开口往下凹函数)
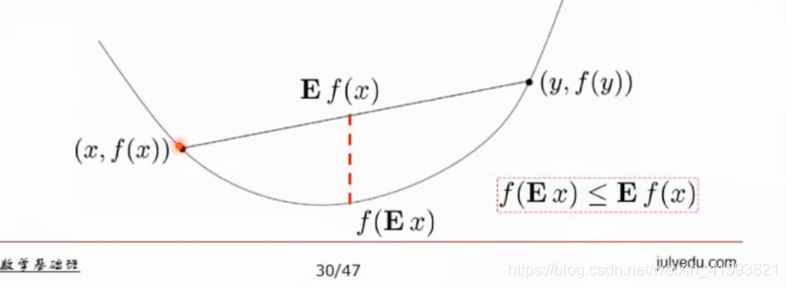
连线上的一点的期望比期望的值大
(期望差不多是平均值)
xy函数值大于函数值的平均值
2. 绝大多数不等式的起源都是这个不等式
3. 只要是凸函数或者凹函数就能够用凸优化
4. 条件概率公式和全概率公式

5. 常见概率分布
6. 泊松分布比较像电商的商品,因为商品某一价格区间的商品比较多
7. 正态分布哪里都有,误差基本上就是正态分布,身高是正态分布
8. 概率和统计的关注点不同
9. 知道条件推断总体情况:概率
10. 数理统计 知道分布但是不知道均值方差

概率统计和机器学习是天然地相关,如果抽样都不对,算法肯定构造地不对,进而出错。
今天上计算几何,说道人工智能是在 L 空间上考虑问题,为这个空间选取合适的基函数,进而考虑问题会简单许多
13. 
16. 误差衍生出不同的损失函数定义方式(面试题)
17. 协方差可以写成期望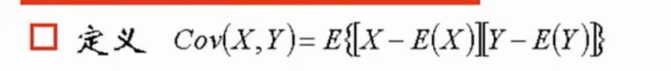

18.
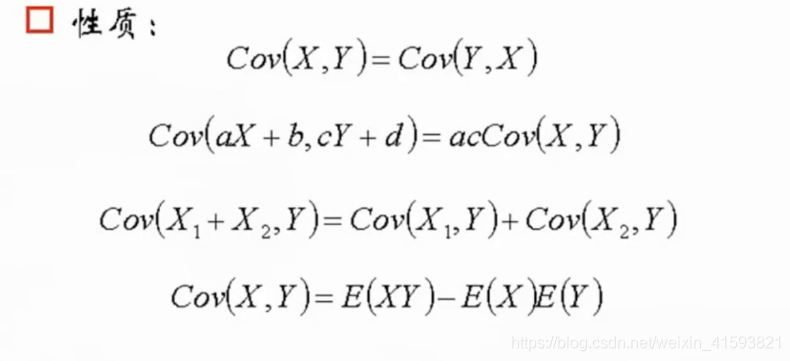
19. 协方差一般用于选择特征,协方差近似于1时特征比较好,但是协方差近似于0时可以将该特征丢掉
20. 相关系数是特征去特征化后的向量的夹角,cos是1当然相关系数是1,也就是线性关系
21. cos是0当然相关系数是0那就是垂直,两个向量完全没有关系
22.
r=cov(X,Y)/sqrt(Var(X)*Var(y))

23. 向量a与b的内积实际上是a在b上的投影
24.



25. 去均值化是很好的预处理方法
26. 为什么协方差是内积
求x和y的协方差就是去均值化,每个值减去期望,减完之后做内积,那就是几何意义
1:37:54
