我们很早就学过,圆的面积计算公式:

但是以前从没想过他是怎么推导来的,今天突发奇想,用微积分推导了一下,然后上网看了下高手们的推导,真的是各种方法无奇不有啊,于是就有了写这篇文章的冲动,总结下各种计算圆面积的方法。
不需要常数π的方法
计算圆的面积中有一个重要常数π,现在假设我们不知道π的值,该怎么计算圆的面积呢?
蒙特卡罗方法(或飞镖法)
不知道常数π的值,也就没法直接求出圆的周长和面积,很好想到的一个方法就是:将圆镶嵌在一个正方形中,然后求出圆占这个正方形面积的百分比:

你可以胡乱朝这个区域投掷飞镖,当飞镖数量足够大,并假设飞镖投到这个区域任意位置的概率是一样的,那么你最后就可以通过飞镖数量求出圆占整个正方形面积的比,设圆的半径为r,正方形面积为:

由知道了比值,自然就可以算出圆的面积
需要常数π的方法
常数π是个重要的常数,它表示圆的周长C和圆的直径d之比:

如果要用公式:

计算圆的面积,当然需要知道π的值。
知道了π的定义,最简单的办法就是滚粗法:

操作起来就是:
先用绳子围绕标准圆一周,然后测量绳子长度:

接着找准圆心,然后用尺子测出圆的直径:

这两的比值就是常数π了。当然为了更好的精确度,可以采用多次测量取平均值的方法。
其实上面讲到的蒙特卡洛方法也可以用来计算常数π,只需将圆的半径设为1就好。
还有一种经典的蒙特卡洛方法,叫做蒲风投针实验:
设针的长度是l,平行线之间的距离为t,x为针的中心和最近的平行线的距离,θ为针和线之间的锐角。

可以推导:

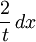
而
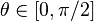
的概率密度函数为:

x和θ两个随机变数互相独立,因此两者结合的概率密度函数只是两者的积:

针和线相交时:

求上式的积分,得到针和线相交的概率:

即抛n针,其中有h针和线相交的概率为:
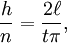
由此可以得到π:

具体操作时,我们可以取t=2l,然后投掷n针,除以针和线相交的次数h,就得到π:

当然还有更多计算π的方法,像数列求极限等,感兴趣的请参考这里
好了,解决了常数π,下面回到正题,如何计算圆的面积?
剪纸法
剪纸法的思想就是化整为零,再重新拼接。

将一个圆剪成很多小的扇形,然后再将其拼成如上图的一个矩形,由于圆的周长是2πr,蓝色和黄色各占一半,所以拼成的长方形的长约为π*r,而长方形的宽约为圆的半径r,所以圆的面积等于长方形的面积:

变形法
其实这个方法和上个方法基本思想是一样的:圆的面积我们不知道,那能不能把圆转换成我们熟悉的形状呢?比如三角形:

三角形的面积公式我们知道,那与它等价的圆的面积自然也就能计算了:

微积分法
大学里学了微积分,用微积分来计算圆的面积,那不是拿着刀俎,鱼肉随便切吗。不过虽然都是用微积分,出发思想不一样,解法也不一样。
洋葱法
使用微积分,我们将圆象洋葱一样分为薄圆环,递增地求出面积。

对“洋葱”,以 t 为半径的无穷薄圆环,贡献的面积是 2πt dt,周长的长度乘以其无穷小宽度。这样对半径为 r 的圆给出了一个初等积分:

极坐标法
极坐标也是一种变换的方法,就像傅里叶变换一样,极坐标变换将直角坐标系下看似复杂的东西变成极坐标系下极其简单的东西,就像在直角坐标系下的一个圆环,在极坐标系下却是长方形:

唯一要注意的是,直角坐标系下的面积微元为:dxdy,而极坐标下却是:tdtdθ,不懂可以参考这里
使用极坐标下的二重积分,积分函数为f(x)=1, 积分区域为圆C,则:

分割伞形法
类似于洋葱法,我们也可以把圆分割为一系列小的伞形区域,则每个区域的面积近似为二分之一的弧长(rdθ)乘以半径r:

然后将dθ从0到2π积分,就可以计算出圆的面积:

半圆法
我们知道,圆的方程为:

由此可得,当y>0时,半圆的方程为:

对函数y从-r到r积分,由积分的定义知,积分的结果为二分之一圆的面积。
要计算:

我们先假设:

则:


那么:

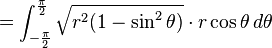
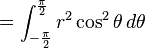



当然,你可以通过mathmatica,直接得到结果:

总结
以上的一些方法,归根结底就两类思想:要么是转化的思想,将圆转化为熟悉的图形计算,要么是微积分的思想,把圆细分为微单元,然后再将这些微单元相加。一个简单的圆面积公式,都有这么多的解法,数学的魅力就在这里。
参考文献
wikipedia
圆的面积
calculus proof for the area of a circle
计算圆周率-Pi
布丰投针问题
圆周率
